Researcher @ North Dakota State University

Summary

• Proposed an empirical likelihood test for detecting community structure in both weighted and unweighted networks, addressing limitations in conventional hypothesis testing approaches focused primarily on unweighted networks.
• Utilized R programming for advanced statistical analysis, including the computation of test statistics, empirical likelihood ratio distributions, and p-values, while evaluating type I error rates and the power of the empirical likelihood test against traditional statistical frameworks by conducting 500 simulations.
• Extended simulations to weighted networks using Beta and Gamma distributions for edge weights, analyzing test accuracy and power for different probabilities.

Abstract

Network data, characterized by interconnected nodes and edges, is pervasive in various domains and has gained significant popularity in recent years. From social networks and transportation networks to biological networks and communication networks, network data has become a valuable source of information for understanding complex systems. A prominent feature of many network data sets is the presence of community structure.

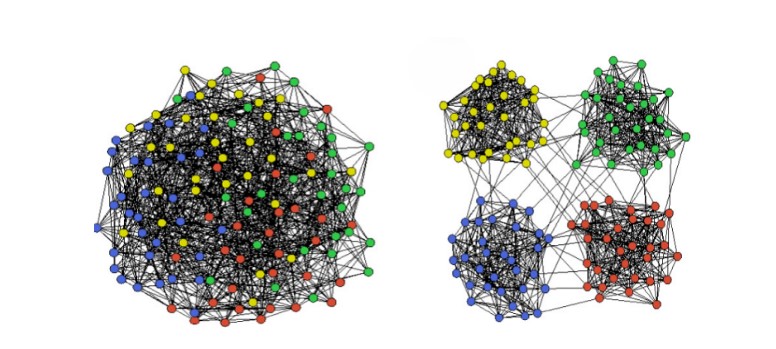
Identifying and understanding the community structure in network data is a critical task in network analysis as it can provide insights into the organization, function, and dynamics of complex systems and facilitate applications such as targeted marketing, disease propagation modeling, anomaly detection, and resource allocation, among others. Community detection techniques, such as modularity optimization, hierarchical clustering, and spectral clustering, are commonly used to uncover and analyze communities in network data. When analyzing the structure of communities within networks, it is common to use hypothesis testing to determine the significance of the observed network structure. Currently, available techniques predominantly address unweighted networks. However, in real-world scenarios, numerous networks comprise weighted connections. In this research, we investigate hypothesis testing for community structure within networks of varying types, considering both weighted and unweighted networks. We propose an empirical likelihood test as a novel approach for detecting community structure in network data. The empirical likelihood method is a statistical technique that does not require any assumptions about the underlying data distribution, making it flexible and robust to different types of network structures. We established the distribution of the empirical likelihood ratio for the null hypothesis and characterized the power of the test. We conducted extensive simulations to evaluate the performance of our iiiproposed empirical likelihood test for community structure detection in network data. Our simulations involved varying network sizes, densities, and community structures to assess the test’s performance under different scenarios. The results of our simulations demonstrated that our empirical likelihood test consistently outperformed existing methods in terms of statistical power. Further validation and real-world applications of our proposed approach can contribute to the advancement of network analysis techniques and aid in understanding complex systems that exhibit community structures.